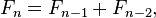Graph Coloring

Graph Coloring: 

In Graph Theory, graph coloring is a special case of graph labeling. It is an assignment of labels traditionally called "colors" to elements of a graph subject to certain constraints. In the easiest form it is a way of coloring the vertices of a graph so that no two adjacent vertices share the same color, this is called vertex coloring. An edge coloring assigns a color to each edge so that no two adjacent edges share the same color, and a face coloring of a planar graph assigns a color to each face or region so that no two faces that share a boundary have the same color. 

A proper vertex coloring of the Petersen graph with three colors

The convention of using colors originates from coloring the countries of a map, where each face is literally covered. By planar duality it became coloring the vertices, and in this form it generalizes to all graphs. For example: In mathematical and computer representations, it is typical to use the first few positive or nonnegative integers as the colors. In general we can use any finite set as the "color set." Graph coloring enjoys many practical applications as well as theoretical challenges. Beside the classical types of problems, different limitations can also be set on the graph, or on the way a color is assigned, or even on the color itself. It has even reached popularity with the public in the form of the popular number game Sudoku. 

There are twelve different ways to color the map from above using three colors. 

A coloring using at most k colors is called k-coloring. The smallest number of colors needed to color a graph G is called its chromatic number, and is often denoted X(G) or Y(G). The chromatic number of a graph G is the smallest number of colors needed to color the vertices of G so that no two adjacent vertices share the same color. 

Examples: 

Examine Questions: Find the chromatic number for each graph listed below?  

Citations: Wikipedia, and Google images

Stable Marriages

The stable marriage problem is another classic appreciation of discrete mathematics to social networks. 

Suppose that you have been hired to be a matchmaker with n men and n woman who wish to be paired up with their perfect matches. Each man provides the matchmaker with a list of the woman ranking from first choice to last choice, as same for the woman. 

The matchmakers job is to provide a way to pair up the n men and n women in such a way so no man or woman is left behind. 

The stable marriage theorem states that your job can always be accomplished, no matter how the men and women have ranked one another. This theorem provides an algorithm that accomplishes your task. 

In round 1: every man proposes to his first choice. those woman who receives the offers tentatively accept the best offer and tell the other men not to come back. The rejected men then propose to their next choice, and the women then tentatively accept the best offer they have so far received and tell the other proposers to go away. This process continues until every man and woman are paired up. 

Example One: Suppose the matchmaker receives the following list: 

man 1 (3,1,4,2,5)

man 2 (1,3,5,2,4) 

man 3 (5,4,3,2,1)

man 4 (1,5,4,2,3)

man 5 (3.4.5.1.2)

woman 1 (3,5,1,4,2) 

woman 2 (3,1,2,4,5)

woman 3 (1,2,3,4,5)

woman 4 (5,3,1,2,4)

woman 5 (5,4,3,2,1)

 Use the stable marriage algorithm to find a stable parring. 

Answer: Men 1,2,3,4 and 5 will propose to women 3,1,5, 1, and 3 respectively. Woman 1 rejects man 2, woman 3 rejects man 5. So then men 2 and 5 propose to women 3 and 4 respectively, but man 2 is rejected again because woman 3 is already taken. Man 2 now continues to move down his list to woman number 5, who accepts him and rejects man number 3. Now man 3 proposes to woman 3, who rejects him. Then man 3 proposes to woman 2 who accepts his offer. WIth no man or woman unattached, the algorithm terminates with stable pairings: 

man 1 with woman 3, man 2 with woman 5, man 3 with woman 2, man 4 with woman 1, and man 5 with woman 4. 

Examine Question: Suppose the matchmaker receives the following list: 

man 1 (c, a, d, b, e)

man 2 (a, c, e, b, d) 

man 3 (e, d, c, b, a) 

man 4 (a, e, d, c, b)

man 5 (c, d, e, b, a)

woman a (3,1,2,4,5)

woman b (3, 5, 1, 4, 2)

woman c (5,3,1,2,4)

woman d (1,2,3,4,5)

woman e (5,4,3,2,1)

A. Use the stable marriage algorithm to find a solution pairing. (men proposes to women)

B. Find another stable marriage obtained by having the women propose to the men. 

RSA Method of Cryptography

RSA: is a crypt o-system, which is known as one of the first practicable public-key crypt o-systems and is widely used for secured data transmission. This method was named after three mathematically trained computer sciences, Ronald Riverst, Aid Shamer, and Lenorad Adleman, who discovered this method in 1977.

In the crypt o-system the encryption key is public and differs from the decryption key which is kept a secret. 

How it works: The bank publishes two numbers on its website, n and e (as in encipher), n and e are about 2000 digits long. 

1, Write your plain text should be under 1000 characters

for example: quiz today   

2. Convert your plain text to a number m (under 2000 digits) by replacing each letter with its 2-digit position in the alphabet

for example: 172109262015040125

3. Computer cipher text C=M raised to the e power mod n. Your the one emailing the C to the bank. 

4. When the bank receives your C, it uses a magic secret number d ( as its decipher) and computes C raised to the d mod n, which equals M. Then it converts M back to your plain text. 

The Encryption: An example of this is: if Brittany transmits her public key (n,e) to Billy and keeps the private key secret. Billy then wishes to send message M to Brittany. He first turns M into an integer m, such that 0 ≤ m < n by using an agreed protocol of the system. he then computes the cipher text c 

corresponding to , then Billy transmits c to Alice. 

The Decryption: Brittany can recover m from c by using her private key exponent d from the formula 

. Given m, she can recover the original message M.

Example One: Compute the following RSA method where p=5 and q=29. Find e and f, and also d to figure out what the value of M will be? 

To find the value of n we multiply p by q. 

so since p=5 and q=29 so (p)(q)=145. 

Now we need to find (n)

(145) = 4 x 28 = 112

We pick d=3 and then find e and f so that 

ed + (n) f =1

3 e + 112 f  =1

3(-37) + 112(1) =1

so e = -37

Now we send the message to M=2. 

The sent message is 

.

Exam Question: Compute the following RSA method where p=3 and q =7. Find e, f. and d to figure out what value M with encryption and decryption? 

Citations: Wikipedia and Our Math notes 

The Chinese Remainder Theorem:

The Chinese Remainder Theorem: is a result of congruences in number theory and some aspects of abstract algebra. It was first published in the 3rd to 5th centuries by Chinese mathematician Sun Tzu. 

The Chinese Remainder Theorem: says if m (one) and m (two) are relatively prime then the system of congruences 

has a unique solution mod m (one) m (two). 

"max" + "may"= 

Example: Find the unique solution to the following congruences: 

so, now we assign all the letters to a specific number,

since (11,9) =1, then there exists x and y so that 

11x+9y=1

using Euclid's formula: we see that 11(5) + 9(-6) = 1

so by this formula we see that x=5 and y= -6. 

Now we will use the "max" + "may" formula: 

=11(2)(5)+ 9(6)(-6)

=  110 - 324

= -214

therefore N=83. 

Example: Find the unique solution to the following congruences: 

so now we assign the letters to a specific number, 

since (5,3) =1 then there exists x and y so that

5x + 3y =1

using Euclid's formula: we see that 5(2) + 3(-3) =1

so by this formula we see that x=2 and y=-3. 

Now we will use the "max"+ " may" formula: 

= 5(2)(2) + 3(3)(-3)

= 20 + -27

= -7

therefore N = 8

Quiz Question: Find the unique solution to the following congruences: 

using the chinese remainder theorem and the "max" + "min" formula. 

.

Credit due to: wikipedia and my class notes

Modular Arithmetic

MODULAR ARITHMETIC: 

Modular Arithmetic is the mathematics of remainders. 

 if m l a-b the number m is called the modulus. 

A common example for Modular Arithmetic is Clock Arithmetic: 

There is an additive law to modular arithmetic that says: 

There is also a commutative law to modular arithmetic that says: 

Example: What is 38 mod 12?

So what you do is divide 12 into 38 and see what the remainder is, 

Example: What is 59 mod 4? 

Examine Question: What is 83 mod 5? 

There are two different tricks to finding mod's the first method is called the casting out nines method: 

the casting out nines method states that for a positive integer x, we define S(x) to be the sum of the digits of x. 

Example: What is S(5409)?

So we need to add all the number in S(x) together and we get 5+4+0+9=18

Now we claim: that 

so using our claim we get 

Examine Question: What is S(1688)?

The second method is just like the casting out of the nines method but using mod 11. So for a positive integer x, we define S(x) to sum of the digits of x. 

Example: What is S(13748)? 

1-3+7-4+8=13

Now we claim that

so using our claim we get 

Examine Question: What is S(34693)?

Work cited to: our lecture notes 

Whats that, its the Euclidean Algorithm

 The Euclidean Algorithm 

• The Euclidean Algorithm is a method for computing the greatest common divisor (gcd) of two integers. It is named after the Greek mathematician Euclid, who described it in books VII and X of his elements. 
• The GCD of two positive integers is the largest integer that divides both of them without leaving a remainder.

In its simplest point, Euclid's algorithm starts with a pair of positive integers, and forms a new pair that consists of the smaller number and the difference between the larger and smaller numbers. The process repeats until the numbers in the pairs are equal. That number than is the greatest common divisor of the original pair of integers. 

                                                  How to set up the Algorithm: 

We will be given two positive integers a and b. We then divide a by b and get a remainder r. If r equals 0, the your b will become your gcd of the two integers a and b. 

Question: When does the remainder stop, will it ever stop? 

Answer: At each round of the algorithm the remainder will go down at least by one, so therefore r will eventually equal zero. 

Exercise: What is the gcd (65, 40)?

65 = 40 (1) + 25

40 = 25 (1) + 20

25 = 20 (1) + 5

20 = 5 (4) + 0

since the remainder is 0 the gcd (65, 40) = 5. 

Exercise: What is the gcd (168, 40)?

168 = 40 ( 4) + 8

40  =  8  ( 5 ) + 0

since the remainder is 0 the gcd (168, 40) = 8.

Potential Examine Question: What is the gcd ( 239, 19)? 

Citations;
1.http://en.wikipedia.org/wiki/Euclidean_algorithm
2.http://www.math.rutgers.edu/~greenfie/gs2004/euclid.html

Fibonacci Numbers/Recurrences

Fibonacci Numbers: 

The Fibonacci Numbers are named after Leonardo Fibonacci. Fibonacci numbers are closely related to Lucas numbers, but I am going to be talking more about the Fibonacci numbers. 

The Fibonacci Numbers are the numbers of this sequence 

The first two numbers in the Fibonacci sequence are 1 and 1, or 0 and 1, depending on the chosen starting point of the sequence, and each subset number is the sum of the previous two.  

Example: Find the next number of the Fibonacci sequence. 

• The two is found by adding the two previous numbers before it ( 1+1) 
• The three is found by adding the two pervious numbers (1+2)
• And the five is (2+3) 
• And so on 

What is the next number of the sequence after 144?

Well if we add (89+144) we get 233. 

What is the next number of the sequence after 233?

The answer should be 377.

The first twenty one Fibonacci F_n for n = 0,1,2,....,20 are: 

F0	F1	F2	F3	F4	F5	F6	F7	F8	F9	F10	F11	F12	F13	F14	F15	F16	F17	F18	F19	F20
0	1	1	2	3	5	8	13	21	34	55	89	144	233	377	610	987	1597	2584	4181	6765

which is defined by the recurrence relation 

Example: Using the recurrence relation find the next number from the picture below?

Find the next number using the recurrence relation?

Your answer should be 17711

                                                        Recurrence:

Example: Suppose I have a recurrence, defined by initial conditions 

 and  

 where 

we have the recurrence 

Using this formula we can generate the next a numbers ( which i am not going to do, but you may do it, by plugging in 3 for n, and 4 for n, and so on.) 

Now we need to find a polynomial from the given equation. So we get the polynomial 

and this can be factored into: 

For the roots of the polynomial we will change both signs of the factored polynomial so root one =3 and root two =-2. Therefor for all n greater than or equal to 0, we get 

We need to make sure the recurrence works so we need to figure out what the constants are. When n=0 we get the equation

and when n=1 we get the equation

Now that we have two equations we can use the elimination method or the substitution method to figure out what c one and c two is. So by doing either methods we will get 

Now we put it all together to get our closed form recurrence: 

Quiz Question:

Suppose I have a recurrence, defined by initial conditions

 and

 where 

we have the recurrence 

Find the roots, and constants and final equation?

Citations: 

wikepedia, mathURL, math is fun, discrete mathematics