Fibonacci Numbers:
The Fibonacci Numbers are named after Leonardo Fibonacci. Fibonacci numbers are closely related to Lucas numbers, but I am going to be talking more about the Fibonacci numbers.
The Fibonacci Numbers are the numbers of this sequence
The first two numbers in the Fibonacci sequence are 1 and 1, or 0 and 1, depending on the chosen starting point of the sequence, and each subset number is the sum of the previous two.
Example: Find the next number of the Fibonacci sequence.
- The two is found by adding the two previous numbers before it ( 1+1)
- The three is found by adding the two pervious numbers (1+2)
- And the five is (2+3)
- And so on
What is the next number of the sequence after 144?
Well if we add (89+144) we get 233.
What is the next number of the sequence after 233?
The answer should be 377.
The first twenty one Fibonacci Fn for n = 0,1,2,....,20 are:
which is defined by the recurrence relationF0 F1 F2 F3 F4 F5 F6 F7 F8 F9 F10 F11 F12 F13 F14 F15 F16 F17 F18 F19 F20 0 1 1 2 3 5 8 13 21 34 55 89 144 233 377 610 987 1597 2584 4181 6765 - Example: Using the recurrence relation find the next number from the picture below?
-
- Find the next number using the recurrence relation?
- Your answer should be 17711
- Recurrence:
- Example: Suppose I have a recurrence, defined by initial conditions
- we have the recurrence
- Using this formula we can generate the next a numbers ( which i am not going to do, but you may do it, by plugging in 3 for n, and 4 for n, and so on.)
- Now we need to find a polynomial from the given equation. So we get the polynomial
- and this can be factored into:
- For the roots of the polynomial we will change both signs of the factored polynomial so root one =3 and root two =-2. Therefor for all n greater than or equal to 0, we get
- We need to make sure the recurrence works so we need to figure out what the constants are. When n=0 we get the equation
- and when n=1 we get the equation
- Now that we have two equations we can use the elimination method or the substitution method to figure out what c one and c two is. So by doing either methods we will get
- Now we put it all together to get our closed form recurrence:
- Quiz Question:
- Suppose I have a recurrence, defined by initial conditions
- we have the recurrence
- Find the roots, and constants and final equation?
- Citations:
- wikepedia, mathURL, math is fun, discrete mathematics
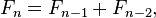
















No comments:
Post a Comment