The Principle of mathematical proofs (PMI) is not an easy proof at first, these types of proofs take practice. To set up (PMI) we need to choose a
It is important that the structure of the proof is correct. In the induction step we are assuming
Example: Prove 1+2+3+.....+100=? For all n in N,
Proof by PMI:
Base Case: we must show
LHS: (left hand side)
RHS: (right hand side)
Right hand side and left hand side =1 so the base case is true.
Induction Step: Suppose that
It is sometimes easier to work out the first steps to get a sense of how to prove the general inductive step, like i did up above.
Potential Exam Question: For all n greater than of equal to Z, Prove the following statement:
Citations: Professor Aaron Wong Proof Notes / Professor Arthur T. Benjamin's Video notes
.png)




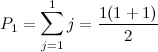













No comments:
Post a Comment