The Multinomial Coefficient
Defining it looks like
but it has an extra set of
parentheses around and it is the number of ways to choose k objects from a set of n objects, where order is not important, but repetition is
allowed.
The equation is
Lets try a Couple of examples using this formula:
Example One: Find
the number of solutions to the equation a + b + c = 40, where a, b, and c are
all non-negative integers.
Example Two: Suppose you have 15 ice cream
flavors and you want a cup of five scoops, they can be the same flavor. How
many ways can we choose the flavors?
Example Three: How many
ways can we arrange the letters Richelle?
Well we see that there are two
L’s and two E’s one R, one I, one C and one H. So we can use the other
equation, which introduces the multinomial coefficient, the equation is
There are eight letters in
Richelle. So there are
So the answer to how many ways
we can arrange Richelle is
Example Four: How many ways can you arrange the letters in
Halloween?
There is 1 H, 1 A, 2 L’s, 1 O, 1
W, 2 E’s and 1 N. in Halloween.
The Multinomial Theorem states:
Where a and b are non-negative
numbers that sum up to n. We will use this theorem later.
Test Question: How many ways can
you arrange the letters in Nevada State College, you can count them as all one
word?
Test Question: Find the number of
solutions to the equation a + b + c + d +e + f =150, where a,b,c.d.e and f are
all non-negative integers?
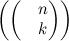




No comments:
Post a Comment